对 Quadrilateral Interpolation, Part 1 的证明

最近在模拟2D像素阴影时，遇到了一个问题，对于任意形状的凸四边形，要如何计算其UV才能让最终的效果看起来正常？（想知道不正常的效果是什么样子？您也可以在下文中的连接中找到对应的图片。）

一番搜索之下，找到了如下链接：
https://www.reedbeta.com/blog/quadrilateral-interpolation-part-1/

这里作者提供了一个通用的公式用于计算UV值，但是作者并没有解释这个公式是如何得来的。本文将试着证明该公式。

首先，我们先看一下作者提供的公式：

注意，这里的结果需要对4取模。当时，，当时，。

同时，让我们看一下作者在这篇博客中提到的：

It’s well-known that to do perspective-correct interpolation for a triangle, you must calculate ,, and at each vertex, interpolate those linearly in screen space, then calculate and at each pixel. GPU rasterizers do this automatically, behind the scenes, for every interpolated attribute.

若您对这段话仍有疑问，建议参考此篇文章：
https://www.cnblogs.com/straywriter/articles/15889273.html

让我们看一下这个链接里是如何计算uv的。它首先在 Vretex Shader 中定义了一个Varying的vec3变量。

这个变量对四边形的每个顶点都会计算一次。

然后，我们的GPU会负责把这个uvq变量进行线性插值。之后，我们在 Fragment Shader 中访问uvq时，它就已经是根据三角形三个顶点的uvq值插值而成的新值了。

之后，它在 Fragment Shader 中使用uvq.xy / uvq.z来计算当前 Fragment 所应该采样的 UV 值。

如果，我们设 则 Vertex Shader 中的uvq就可以写成 。然后之后我们在 Fragment Shader 中我们相当于计算了 ，

到这里，我们能很明显看出来了，这里其实是在手动模拟透视矫正插值。

那么，这个 究竟是个什么？

首先我们需要知道我们面临的问题是什么。

首先，我们有一个在图像平面（image plane）的四边形形状，而我们的目标就是找到一个平行四边形，使其投影到图像平面的形状恰好和我们要求的四边形重合。

（为什么是平行四边形？因为我们的Texture是矩形，从矩形到平行四边形是仿射变换，仿射变换不会影响我们对uv进行线性插值，具体请参考第一个链接的开头部分。为什么不是矩形？因为平行四边形已经足够我们实现我们的效果？同时使用矩形还需要额外证明一些不必要的东西，同时我们也无法保证真的存在这样的矩形（笔者并未尝试过证明该矩形是否一定存在）。）

而这个z，就是这个平行四边形的四个顶点距离摄像机的距离。

下面，我们就来证明为何这样的Z定义的平行四边形能够在图像平面恰好形成我们需要的四边形。

首先，这个平行四边形的四个顶点肯定都在从摄像机到图像平面四边形的四个顶点所确定的四条直线上。不然这个平行四边形在图像平面上的投影不会是我们所需要的四边形。

现在，我们设这个平行四边形的四个顶点为，且和为两条对角线，这四个点在图像平面上的投影为。

现在我们取其中一条对角线，形成的线段中点记为。点在图像平面上的投影为，我们可以得到下图，其中是摄像机位置。

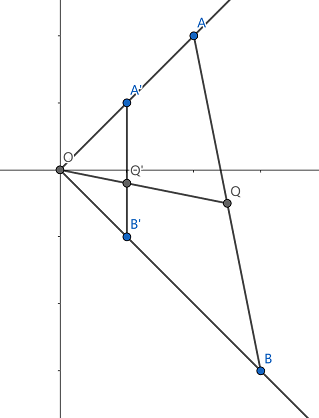
我们设A的坐标为，B的坐标为（这里的坐标代表其在上图中的2D坐标，并不代表其在真实世界坐标系下的坐标。）

可以看出，点A在View空间坐标系下的z坐标，点B在View空间坐标系下的z坐标。

同时，我们有：

这里的和代表在原博客内容中的和（这里我们设AB为和所组成的对角线。）

这里需要证明一下就是我们和的交点。首先因为平行四边形对角线相互平分，而是的中点，所以一定是和的交点。而透视投影保持共线性，所以也是和的交点。

（什么是保持共线性？根据这篇文章的说法，保持共线性指的是变换后，原本在一条直线上的点仍然保持在同一条直线上。（Points on a line remain aligned post-transformation））

点Q的坐标（同样，是指在上图的2D坐标）可以表示为。

因为点、点和点都位于图像平面上，所以它们的（图像平面是距离摄像机为1且与摄像机方向垂直的平面），又因为相似三角形的原理，我们可以算出它们的y坐标，最终它们的坐标为：

又因为

同理

代入

我们有

同理，我们也可以得到

至此，我们得到了对角线两边的点的z值和它到对角线交点长度的关系。我们可以试一下，如果按照原博客的公式，，符合我们的证明结果。

那么，和的关系要如何计算呢？这里需要用到另一个限制，为了保证是一个平行四边形，和的中点必须是同一个点，否则这四个点就不再共面。

首先，因为相似三角形，我们有：

我们设为和共同的中点。

同理

又因为的x均为1。

所以

由此，我们得出了的比例关系，且符合原博客中给出的答案。

可以注意到，这里我们给出的是比例关系，实际上这样的平行四边形是有无穷多个的，这也是符合我们的直觉的，只需要沿着z轴等比放大，我们生成的平行四边形总是可以在图像平面上投影成一样的形状。

笔者对于图形学来说也只是略懂皮毛，数学教育更是可以用悲剧来形容，以上的证明几乎可以肯定包含错误或不准确的地方，如有问题请联系 wlzqkwd#Gmail.com。

最后，让我们以一张笔者目前正在尝试的像素光照的效果作为结尾吧：

本文修改于2026年2月6日，修正了部分公式中的笔误，对于一些之前语焉不详的部分又重新解释了一下，希望能更容易理解一些。